[GSL 강좌 1] 보간법 (Interpolation) - 2

안녕하세요. Numerical Factory입니다.

 

[Numerical Libraries/GSL] - [GSL 강좌 1] 보간법 (Interpolation) - 1

 

지난 시간에는 보간법에 대해 아주 간략하게 설명드렸습니다.

오늘은 지난번 강좌에 이어서 Spline interpolation 실전 예제에 대해서 설명드리려 합니다.

총 11개의 데이터(sine 함수)를 이용해서 1차 미분 함수(cosine 함수)까지 도출해봅시다

 

보간을 하려면 기본적으로 아래와 같이 3가지가 필요합니다.

• Sample Data
• 보간 함수 초기화
• 원하는 데이터 추출

 

이 세가지만 기억하시면 됩니다.

 

GSL Spline 함수를 이용한 보간을 수행하는 코드는 아래와 같습니다.

 

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <gsl/gsl_errno.h>
#include <gsl/gsl_spline.h>

int main(void)
{
     int i;
     double x[11], y[11];
     double xi, yi, yi_deriv1, yi_deriv2;

     // Data Initialization using sine function
     for (i=0; i<11; i++) {
         x[i] = (2.0 * M_PI / 10.0) * i;
         y[i] = sin(x[i]);
     }

     // Spline interpolation using GSL
     gsl_interp_accel *acc = gsl_interp_accel_alloc();
     gsl_spline *spline = gsl_spline_alloc(gsl_interp_cspline, 11);
     gsl_spline_init(spline, x, y, 11);

     for (i=1; i<100; i++) {
         xi = (2.0 *M_PI / 100.0) * i;
         yi = gsl_spline_eval(spline, xi, acc);
         yi_deriv1 = gsl_spline_eval_deriv(spline, xi, acc);
         yi_deriv2 = gsl_spline_eval_deriv2(spline, xi, acc);
         printf("%g %g %g %g\n", xi, yi, yi_deriv1, yi_deriv2);
     }

     gsl_spline_free(spline);
     gsl_interp_accel_free(acc);

     return 0;
}

 

GSL Spline 함수를 이용해서 코드를 작성을 한 이후 코드가 제대로 실행하는지 확인을 하기 위해서는 아래와 같이 컴파일 과정을 진행해야 합니다.

 

Numerical:~$ gcc -o interpol interpol.c -lgsl -lgslcblas -lm

 

이제 GSL spline interpolation을 통해서 얻은 데이터를 그래프화 해보았습니다.

 

Sample Data 를 이용한 Spline Interpolation & 1계 도함수 보간 결과

• + 마크는 우리가 spline interpolation을 위한 Sine 함수의 샘플 데이터입니다.
• 주황색선은 spline interpolation을 통해 얻은 데이터입니다.
• 초록색선은 spline interpolation을 통해 1계 미분값을 얻은 데이터입니다.

그래프만 봤을 때는 11개의 데이터를 활용한 보간과 1계 도함수 값이 보기 좋게 나오는 걸 알 수 있습니다. 

조금 더 수치해석 입장으로 분석을 해보면 보간 데이터와 실제값 간의 잔차를 확인해야 유의미한 결과를 분석할 수 있습니다.

 

먼저 보간 데이터와 실제값과의 차이입니다.

 

0 ~ 2pi 구간에서 약 ±0.0004 수준의 잔차가 발생함을 알 수 있습니다. 이런 결과는 우리가 11개의 데이터를 이용해서 spline interpolation을 진행할 경우 소수점 3번째 자리까지는 확실한 데이터임을 알 수 있습니다.

 

두 번째는 spline interpolation으로부터 구한 1계 도함수 데이터와 실제값과의 차이입니다.

 

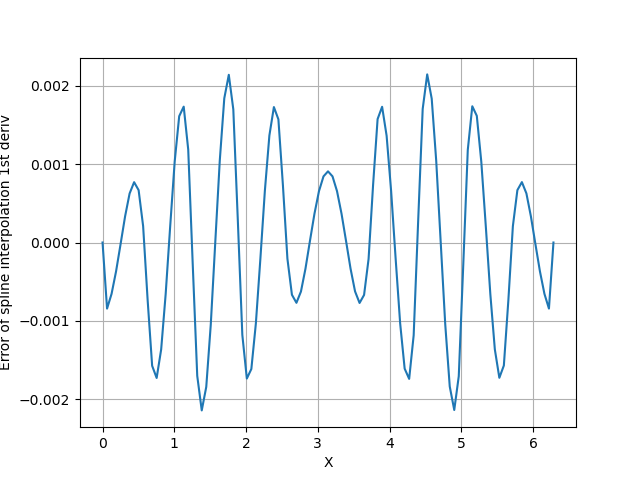
0 ~ 2pi 구간에서 약 ±0.002 수준의 잔차가 발생함을 알 수 있습니다. 우리가 11개의 데이터를 이용해서 spline interpolation을 진행한 후 1계 도함수를 계산할 경우 소수점 2번째까지 믿을 수 있는 데이터를 확보한다는 뜻입니다.

 

우리가 좀 더 정확한 보간 데이터를 확보하기 위해서(더 많은 유효숫자를 확보하기 위해서) 샘플링 수량을 늘리면 됩니다. 하지만 무턱대고 샘플링 수량을 늘리게 되면 불필요한 계산이 진행될 가능성이 높습니다. 적정 수준의 샘플링 수량을 얻기 위해서는 우리가 사용하는 수치 해석 알고리즘 Error Convergence를 파악하면 됩니다.

일반적으로 complete cubic spline의 경우 샘플링 개수가 2배 늘수록 정확도(에러의 수준)는 100배씩 늘어납니다. 이를 이용하게 되면 최적의 샘플링 개수를 확보할 수 있습니다.

 

간단한 GSL 코드를 통해서 적은 데이터를 통해 우리가 원하는 함수의 구간 데이터를 확보할 수 있을 뿐 아니라 확보된 함수의 1계 미분 함수의 데이터도 거의 완벽하게 보간을 할 수 있었습니다. 또한 Error Convergence를 파악할 경우 현재 우리가 원하는 수준의 정확도에 맞는 샘플링 개수를 확보할 수 있음도 알 수 있었습니다.

 

Numerical Factory